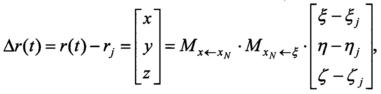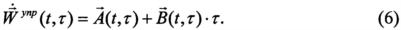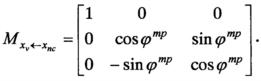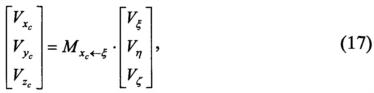РОССИЙСКАЯ ФЕДЕРАЦИЯ ФЕДЕРАЛЬНАЯ СЛУЖБА ПО ИНТЕЛЛЕКТУАЛЬНОЙ СОБСТВЕННОСТИ	(19) RU (11) 2 654 238 (13) C1
	(51) МПК G05D 1/00 (2006.01) (52) СПК G05D 1/00 (2006.01) G06F 17/00 (2006.01)

Статус:	не действует (последнее изменение статуса: 09.08.2022)
Пошлина:	Возможность восстановления: нет.

(21)(22) Заявка: 2017104148, 08.02.2017 (24) Дата начала отсчета срока действия патента: 08.02.2017 Дата регистрации: 17.05.2018 Приоритет(ы): (22) Дата подачи заявки: 08.02.2017 (45) Опубликовано: 17.05.2018 Бюл. № 14 (56) Список документов, цитированных в отчете о поиске: RU 2571567 C2, 20.12.2015. RU 2554568 C2, 27.06.2015. US 20160104382 A1, 14.04.2016. US 8038062 B2, 18.10.2011. US 8103398 B2, 24.01.2012. Адрес для переписки: 143900, Московская обл., г. Балашиха, ул. Карбышева, 8, стр. 3, ФГКВОУ ВО Военная академия РВСН имени Петра Великого МО РФ

(72) Автор(ы): Таныгин Андрей Валерьевич (RU), Горченко Лев Дмитриевич (RU), Байрамов Казым Рашид оглы (RU) (73) Патентообладатель(и): Федеральное государственное казенное военное образовательное учреждение высшего образования "Военная академия Ракетных войск стратегического назначения имени Петра Великого" Министерства обороны Российской Федерации (RU)

(54) Способ управления беспилотным планирующим летательным аппаратом

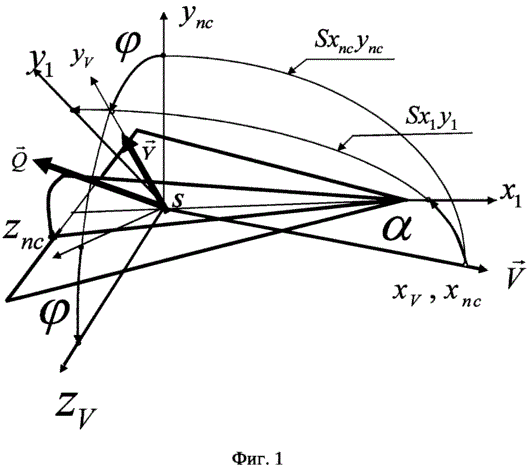
Изобретение относится к области наведения беспилотных планирующих летательных аппаратов (БПЛА) и может быть использовано при создании и эксплуатации таких летательных аппаратов.

Наиболее близким к данному изобретению является описанный способ управления движением БПЛА, базирующийся на следующих основных положениях:

1. БПЛА движется в высоких слоях атмосферы с большой начальной скоростью, обладает существенным аэродинамическим качеством и возможностью автономного управления величиной и направлением аэродинамической подъемной силы путем целенаправленного изменения угла аэродинамического крена ϕ и угла атаки α. На фиг. 1 представлена схема БПЛА с действующими на нее аэродинамическими силами: подъемной силой и силой лобового сопротивления 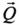, а также показана схема введения угла аэродинамического крена ϕ и угла атаки α с использованием связанной с БПЛА - Sx₁y₁z₁, скоростной - Sx_Vy_Vz_V и полускоростной - 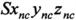систем координат.

2. Управление БПЛА заключается в последовательном наведении на каждую из совокупности опорных точек траектории M_j (j=1, …, N), заданной геодезическими координатами B_j, L_j, H_j, и направлений их пролета, заданных углами азимута A_j и наклона к местным горизонтам θ_j.

3. Наведение БПЛА осуществляется с использованием терминального метода наведения «по требуемому ускорению» [1], который включает решение краевой задачи наведения с целью определения требуемого ускорения, обеспечивающего перевод БПЛА из текущего положения в требуемое конечное, задаваемое в каждой очередной опорной точке траектории. Требуемое ускорение как функция времени движения на оставшейся части пути к опорной точке определяется для управления движением БПЛА в поперечном направлении и реализуется путем придания БПЛА соответствующих значений угла аэродинамического крена и угла атаки . Движение в продольном направлении осуществляется по инерции. Определение и реализация величин углов и осуществляются в каждом цикле наведения T_цн, измеряемом долями секунды, в течение всего времени движения БПЛА к очередной точке наведения.

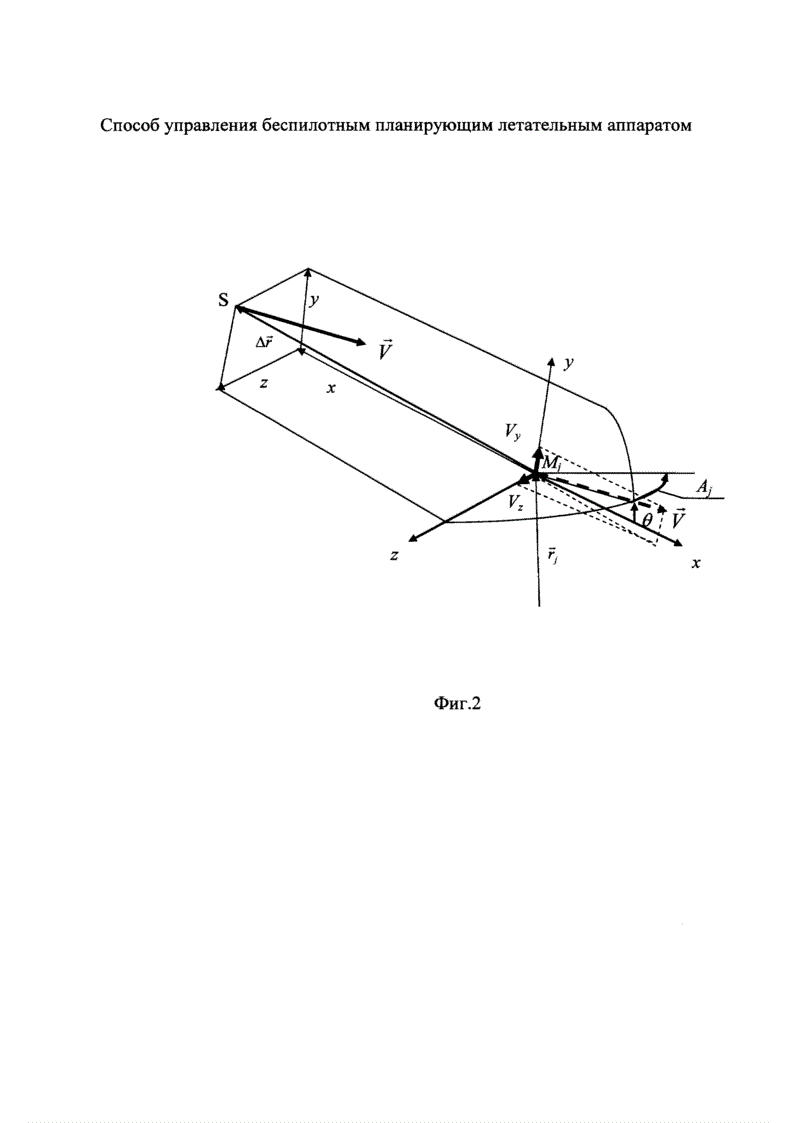
Краевая задача наведения предполагает выбор целевой системы координат, в которой задаются уравнения движения БПЛА и краевые условия. В прототипе в качестве целевой выбрана прямоугольная система координат M_jxyz с началом в опорной точке M_j, осью M_jx, ориентированной азимутом A_j и углом наклона траектории θ_j, осью M_jz в плоскости местного горизонта и осью M_jy, дополняющей систему координат до правой (фиг. 2). Предполагается, что текущие параметры движения БПЛА - r(t), V(t) - в реальном полете определяются бортовой навигационной системой, а при компьютерном моделировании полета БПЛА - из интегрирования системы дифференциальных уравнений, описывающей движение БПЛА. Пусть, например, известны значения текущих параметров движения БПЛА 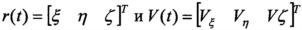в гринвичской геоцентрической относительной системе координат Oξηζ. Из полетного задания известны геодезические координаты опорных точек M_j, преобразуемые в систему координат

Система уравнений движения БПЛА в целевой системе координат M_jxyz при допущении о безынерционном выполнении задаваемых управляющих команд в векторной форме имеет вид:

где кажущееся ускорение БПЛА от суммарной аэродинамической силы разделено на «полезную» часть - требуемое управляющее ускорение и «вредную» часть 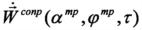- ускорение от силы сопротивления движению БПЛА; - ускорение от силы притяжения Земли в точке M_j.

4. Краевые условия задачи наведения в системе координат M_jxyz задаются в следующем виде:

- в текущей точке траектории или на «левом» конце краевой задачи наведения

где

а матрицы направляющих косинусов - и , связывающие относительную геоцентрическую гринвичскую систему координат Oξηζ с целевой M_jxyz, легко определяются, поскольку известны углы B_j, A_j и θ_j.

Краевые условия в конечной точке траектории или на «правом» конце краевой задачи наведения имеют вид:

Время движения БПЛА на оставшейся части пути к точке наведения T прогнозируется в каждом цикле наведения T_цн с использованием гипотезы о равномерном прямолинейном движении БПЛА на оставшейся части пути:

В краевой задаче требуется на временном интервале [t, t_к]=[0≤τ≤T] определить вектор - функцию , удовлетворяющую краевым условиям (2) и ограничению на величину угла атаки, заданную соотношением:

Решение краевой задачи в аналитическом виде в прототипе получено при представлении требуемого ускорения в форме простой интегрируемой функции - временного полинома первого порядка:

При допущениях, что поле притяжения Земли на участке сближения БПЛА с точкой наведения принимается однородным, а ускорение силы притяжения - равным ускорению в точке M_j-g(r), и неучете вращения Земли, система уравнений (1) декомпозируется на три независимых подсистемы, из которых «полезные» компоненты ускорения определяются в виде проекций вектор-функции (6) на оси M_jy и M_jz целевой системы координат M_jxyz:

оптимальному по затратам энергии (или - для планирующего ЛА - по потерям скорости движения) управлению ЛА при наведении его на цель. Представим их в виде:

где значения коэффициентов A^(y), B^(y), A^(z), B^(z) на любой момент времени из интервала [0≤τ≤T] определяются после интегрирования упомянутых подсистем уравнений с краевыми условиями (2) и (3). В результате определяются программы изменения управляющих ускорений в виде:

Преобразование требуемых ускорений из вида (7), (8) к виду, реализуемому органами управления БПЛА, осуществляется следующим образом. Сначала требуемые ускорения преобразуются в полускоростную систему координат:

где матрица , связывающая целевую систему координат с полускоростной, имеет вид:

а требуемое значение угла аэродинамического крена на момент τ, в качестве которого задается момент из очередного цикла наведения T_цн, например , рассчитывается по формуле:

Требуемое значение угла атаки определяется после определения проекций требуемого ускорения в скоростной системе координат:

где матрица, связывающая полускоростную систему координат со скоростной системой координат, имеет вид:

Однако сначала из выражения

в котором левая часть определена по формуле (12), а в правой части известны значения массы m и характерной площади крыла 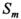БПЛА, значения скорости V, высоты полета H и соответствующей плотности атмосферы ρ, определяется требуемое значение коэффициента подъемной силы .

Требуемое значение угла атаки 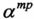определяется с помощью таблиц, представляющих зависимость аэродинамических коэффициентов от высоты H, числа Маха M и угла атаки α. По известным значениям 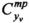, H, M методом итераций определяется требуемое значение угла атаки . По другой таблице определяется соответственно значение аэродинамического коэффициента силы лобового сопротивления , , используемого при математическом моделировании движения БПЛА.

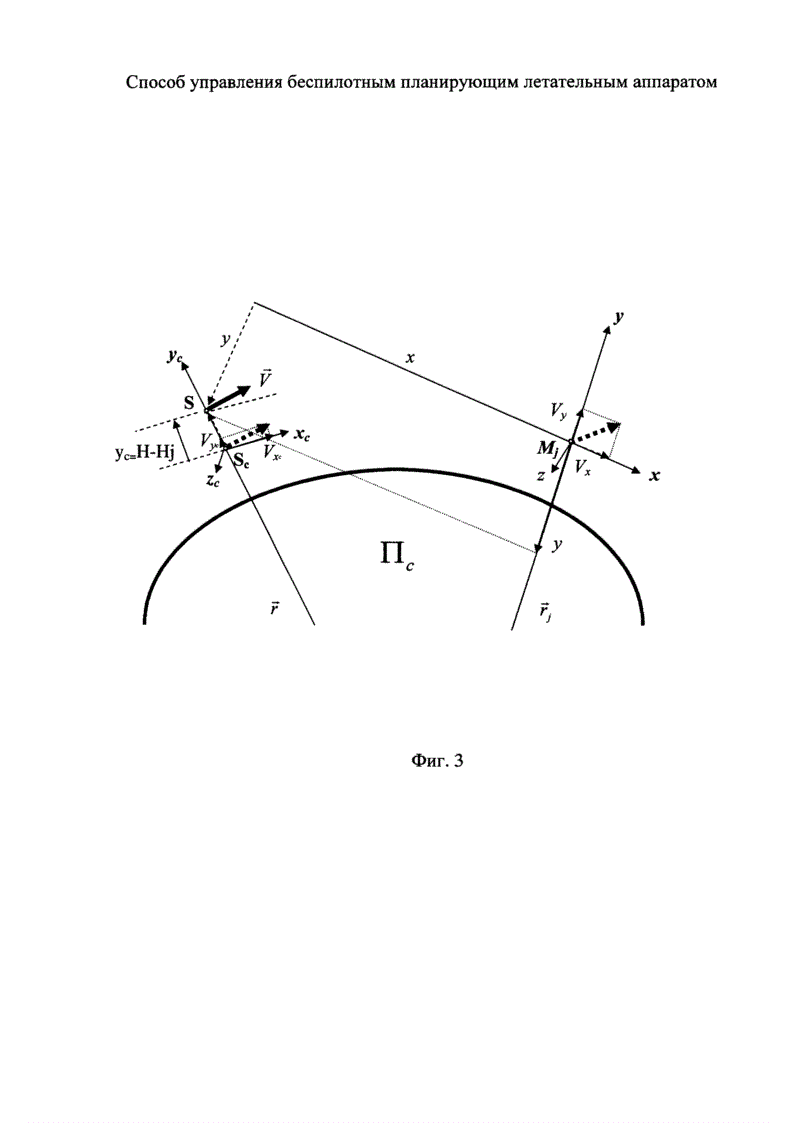
Недостатком ближайшего аналога является его непригодность для управления БПЛА на больших - порядка нескольких тысяч километров - расстояниях от точки наведения. Причиной этому является зависимость величин параметров y, z, V_y, V_z, служащих краевыми условиями в краевой задаче наведения, от положения летательного аппарата в целевой системе координат. На больших удалениях от начала системы координат (фиг. 3) из-за кривизны траектории БПЛА параметры y, z, V_y, V_z принимают очень большие значения и, как следствие (см. формулы (7), (8)), становятся большими значения требуемых ускорений , 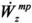и соответственно значение требуемого угла атаки .

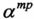В результате условие (5) не выполняется и управление движением БПЛА осуществляется на большей части маршрута при значениях 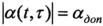. А это приводит к существенным потерям скорости движения из-за сопротивления атмосферы.

Задачей предлагаемого изобретения является устранение указанного недостатка в бортовом алгоритме наведения БПЛА.

Технический результат достигается тем, что в каждом цикле наведения на каждую опорную точку траектории решают краевую задачу наведения, полученные компоненты требуемого ускорения преобразуют в полускоростную и в скоростную системы координат и с их помощью определяют требуемые значения угла аэродинамического крена и угла атаки, краевую задачу наведения решают в сопровождающей системе координат с началом на текущем радиус-векторе центра масс БПЛА на высоте, равной высоте очередной опорной точки траектории.

За счет применения в качестве целевой системы координат в краевой задаче наведения сопровождающей системы координат, в которой краевые условия на левом конце определяются и всегда остаются малыми, требуемые значения ускорения и угла атаки во все время наведения на опорные точки траектории остаются малыми и малыми оказываются потери скорости БПЛА из-за сопротивления атмосферы.

Сущность изобретения поясняется приведенным ниже описанием, фиг. 1-3 и подтверждается примером моделирования траектории БЛА при реализации ближайшего способа и предложенного способа управления в таблицах 1, 2.

Суть предлагаемого способа управления БПЛА та же, что и в ближайшем аналоге, только в качестве целевой системы координат, в которой задаются краевые условия и решается краевая задача, выбирается так называемая сопровождающая системы координат S_cx_cy_cz_c (фиг. 3) с началом на радиус-векторе центра масс БПЛА в точке S_c, высота которой постоянна и равна высоте очередной точки наведения:

Ось S_cy_c системы S_cx_cy_cz_c направлена вдоль радиус-вектора 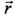от центра масс БПЛА - точки S; ось S_cz_c - по нормали к плоскости П_с, образуемой двумя радиус-векторам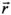и - и , исходящими из центра Земли. Ось S_cx_c дополняет целевую систему координат до правой.

Модель движения БПЛА в краевой задаче наведения на точку M_j в системе координат S_cx_cy_cz_c по форме не отличается от модели (1), но теперь уравнения движения интегрируются при других краевых условиях:

на левом конце -

на правом конце -

На фиг. 3 показано различие величин краевых условий в краевых задачах наведения в одной и той же текущей точке траектории БПЛА в двух описываемых способах управления движением БПЛА.

Координата y_c определяется бортовой навигационной системой в виде , а координата z_c=0.

Проекции вектора скорости на оси системы координат S_cx_cy_cz_c определяются по формуле:

где матрица направляющих косинусов, связывающая относительную геоцентрическую гринвичскую систему координат с текущей сопровождающей системой координат, определяется в каждом цикле наведения в виде:

где

где 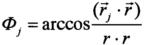, и входящие в выражения (19) векторы и их модули известны из полетного задания и навигационных измерений.

Необходимо отметить, что при сближении БПЛА с каждой опорной точкой значение центрального угла Ф_j между векторам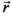и и стремится к нулю и, как следствие, система координат S_cx_cy_cz_c (см. формулы (19)) вырождается. Аналогично вырождаются и величины 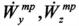(смотри формулы (7), (8)) при T→0. Выходом из этих ситуаций служит «замораживание» расчета направления орта при достижении в процессе наведения выполнения условия Ф_j≤Ф_min - минимально допустимого значения угла, а во втором случае - при достижении условия T≤T_цн - продолжительности цикла наведения.

Значения проекций требуемого ускорения на оси целевой системы координат S_cx_cy_cz_c теперь имеют вид:

Далее алгоритм определения требуемых значений управляющих параметров - угла аэродинамического крена и угла атаки - не отличается от алгоритма описанного выше способа-прототипа. По формулам вида (9), (10), (11), в которых в качестве проекций вектора скорости БПЛА вместо проекций на оси системы координат M_jxyz используются одноименные проекции скорости на оси сопровождающей системы координат S_cx_cy_cz_c, определяются требуемые значения ускорений в полускоростной системе координат и требуемое значение угла аэродинамического крена . Далее по формулам, аналогичным формулам (12), (13), рассчитывается проекция требуемого ускорения на ось Sy_ν скоростной системы координат и определяется требуемое значение аэродинамического коэффициента подъемной силы .

Далее с помощью таблиц определяется требуемое значение угла атаки .

На фиг. 3 представлена схема, иллюстрирующая различия величин текущих параметров движения БПЛА, используемых при решении краевой задачи наведения в двух описанных выше целевых системах координат в качестве краевых условий. Из приведенной схемы видно, что величины y и V_у, определяемые в системе координат M_jxyz, при больших расстояниях текущей точки траектории S от точки M_j существенно больше (по модулю) величин y_c и из-за влияния кривизны траектории на участке движения БПЛА к точке M_j. Следовательно, величины проекций требуемого ускорения в сопровождающей системе координат, вычисляемые по формулам (19), (20), окажутся значительно меньше, чем вычисляемые по формулам (7), (8) в целевой системе координат M_jxyz. Далее цепочки вычислений по двум описанным алгоритмам приводят к существенно различным значениям требуемого угла атаки и, как следствие, к существенно различным величинам силы лобового сопротивления атмосферы. В результате при использовании в краевой задаче сопровождающей системы координат в качестве целевой системы координат уменьшаются потери скорости, увеличивается располагаемая дальность полета БПЛА.

Кроме того, при планировании маршрутов БПЛА большой протяженности количество опорных точек, включаемых в состав данных полетного задания, сводится к минимуму и определяется только конфигурацией маршрута. При этом нет необходимости кроме координат опорных точек задавать требуемые значения азимутов и углов наклона траектории, так как требуемые направления движения БПЛА после пролета опорных точек задаются направлением первой оси сопровождающей системы координат.

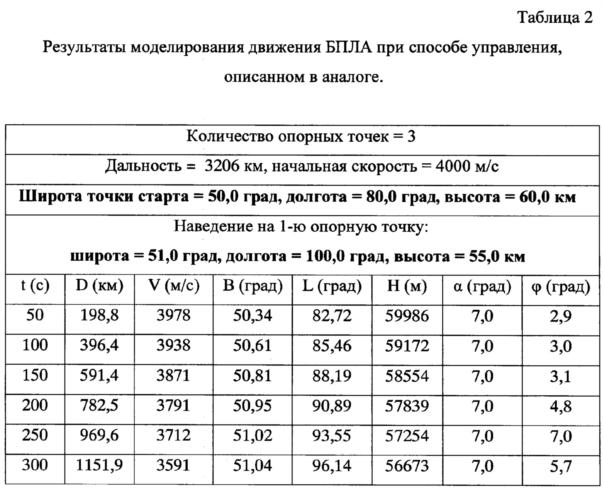
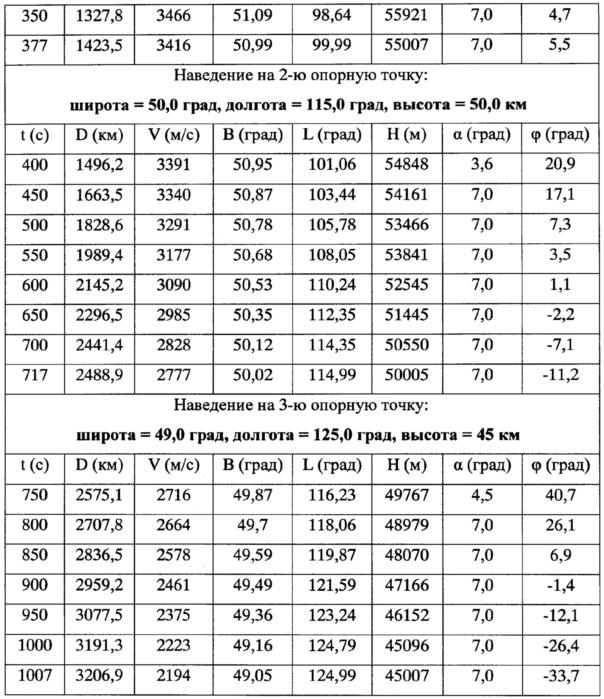
В таблице 1, 2 представлены результаты моделирования движения БПЛА при двух описанных выше способах управления на одном и том же участке пути при одних и тех же начальных условиях.

Источник информации

1. Горченко Л.Д. Метод терминального наведения по требуемому ускорению аэродинамически управляемых летательных аппаратов. Журнал «Полет», №6, М.: Машиностроение, 1999, с 21-24.

Формула изобретения

Способ управления беспилотным планирующим летательным аппаратом, заключающийся в том, что в каждом цикле наведения на каждую опорную точку траектории решают краевую задачу наведения, полученные компоненты требуемого ускорения преобразуют в полускоростную и в скоростную системы координат и с их помощью определяют требуемые значения угла аэродинамического крена и угла атаки, отличающийся тем, что краевую задачу наведения решают в сопровождающей системе координат с началом на текущем радиус-векторе центра масс беспилотного планирующего летательного аппарата на высоте, равной высоте очередной опорной точки траектории.

ИЗВЕЩЕНИЯ

MM4A Досрочное прекращение действия патента из-за неуплаты в установленный срок пошлины за поддержание патента в силе

Дата прекращения действия патента: 09.02.2019

Дата внесения записи в Государственный реестр: 17.12.2019

Дата публикации и номер бюллетеня: 17.12.2019 Бюл. №35